一.前言
在電力電子領域,尤其是在功率因數校正(PFC)的應用中,準確計算交流(AC)電流的有效值(Root Mean Square,RMS)是至關重要的。有效值的計算能夠提供電流在熱效應上等效的直流值,這對於評估電氣設備的性能和安全性至關重要。傳統的RMS計算方法通常涉及複雜的積分運算或者離散傅里葉變換,這些方法在實時計算和資源受限的系統中可能不太適用。遞歸算法以其高效的計算和較低的資源消耗,為AC電流RMS的實時計算提供了一種有效的解決方案。
二.遞歸算法公式詳解
在PFC應用中,我們關注的是交流電流的RMS值,它能夠反映電流在一定時間內的能量平均值。遞歸算法的核心在於利用前一時刻的RMS值來預測和更新當前時刻的RMS值,這樣可以避免對整個數據序列進行重複的計算。具體來說,遞歸算法的公式如下:
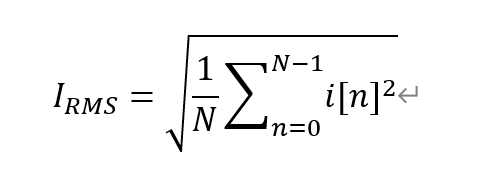
遞歸算法利用前一時刻的RMS值來計算當前時刻的RMS值,公式如下: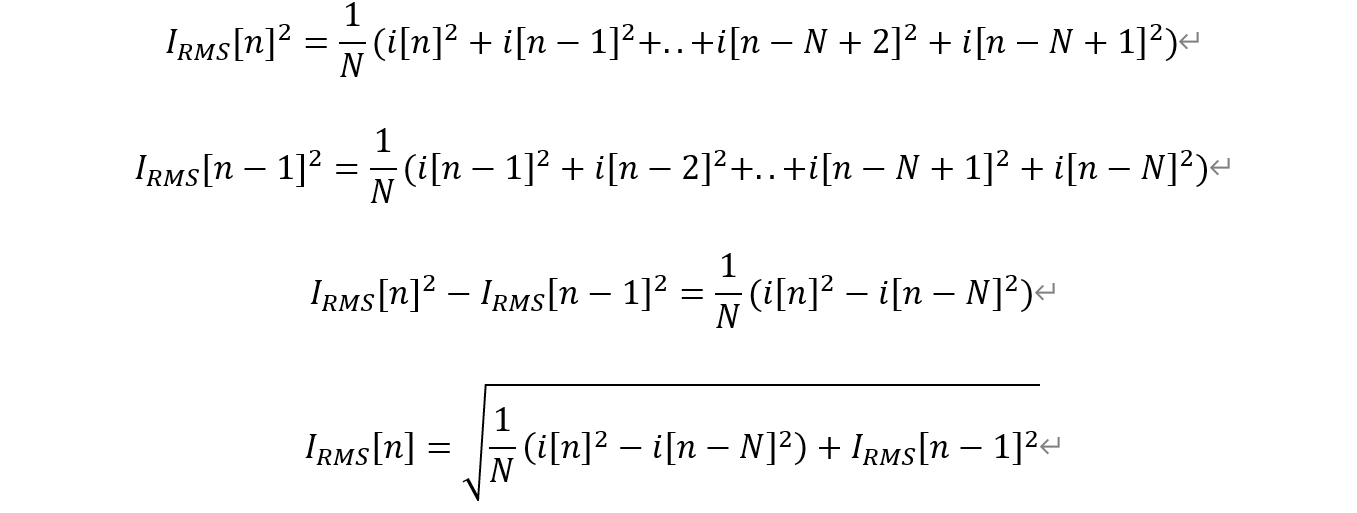
其中,N是樣本總數,它是一個常數,用於歸一化樣本的貢獻。i[k]是當前時刻的電流樣本,它的平方被加到前一時刻RMS值的加權和中。這種方法的優點是,它只需要存儲前一時刻的RMS值,而不是整個樣本序列,從而大大減少了存儲需求。
三.在SR6P6 MCU中實現遞歸算法計算RMS
首先,我們需要初始化RMS值 IRMS[0]。實際應用中,這通常設置為0或者第一個樣本的值,取決於算法的具體實現。
void PFC_MovingRMS_Init(PFC_MovingRMS_t *mrms, uint16_t L)
{
mrms->L = L;
mrms->invL = 1.0f/(L);
mrms->cnt = 0;
for(uint16_t n=0; n<L;n++)
{
mrms->in_sq_L[n] = 0.0f;
}
mrms->out_sq = 0;
}
對於每個新的電流樣本 i[n]i[n],我們需要從PFC電路中採集或者通過模擬數字轉換器(ADC)獲取。使用遞歸公式更新RMS值。這涉及到計算當前樣本的平方,然後將其與前一時刻的RMS值結合起來,計算出新的RMS值。
float PFC_MovingRMS_Update(PFC_MovingRMS_t *mrms, float input)
{
float in_sq = input * input;
mrms->in_sq_L[mrms->cnt] = in_sq;
if(mrms->cnt == (mrms->L -1))
{
mrms->cnt = 0;
}
else
{
mrms->cnt++;
}
mrms->out_sq = mrms->out_sq + mrms->invL * (in_sq - mrms->in_sq_L[mrms->cnt]);
return mrms->out_sq;
}
Iac_RMS= PFC_MovingRMS_Update(&PFC_V_MovingRMS, PFCInputPort.PFC_Iac);
Iac_RMS = sqrtf(temp_f);
將採樣到的AC電流值及計算到的電流有效值上傳到波形顯示工具中,具體波形顯示如下:
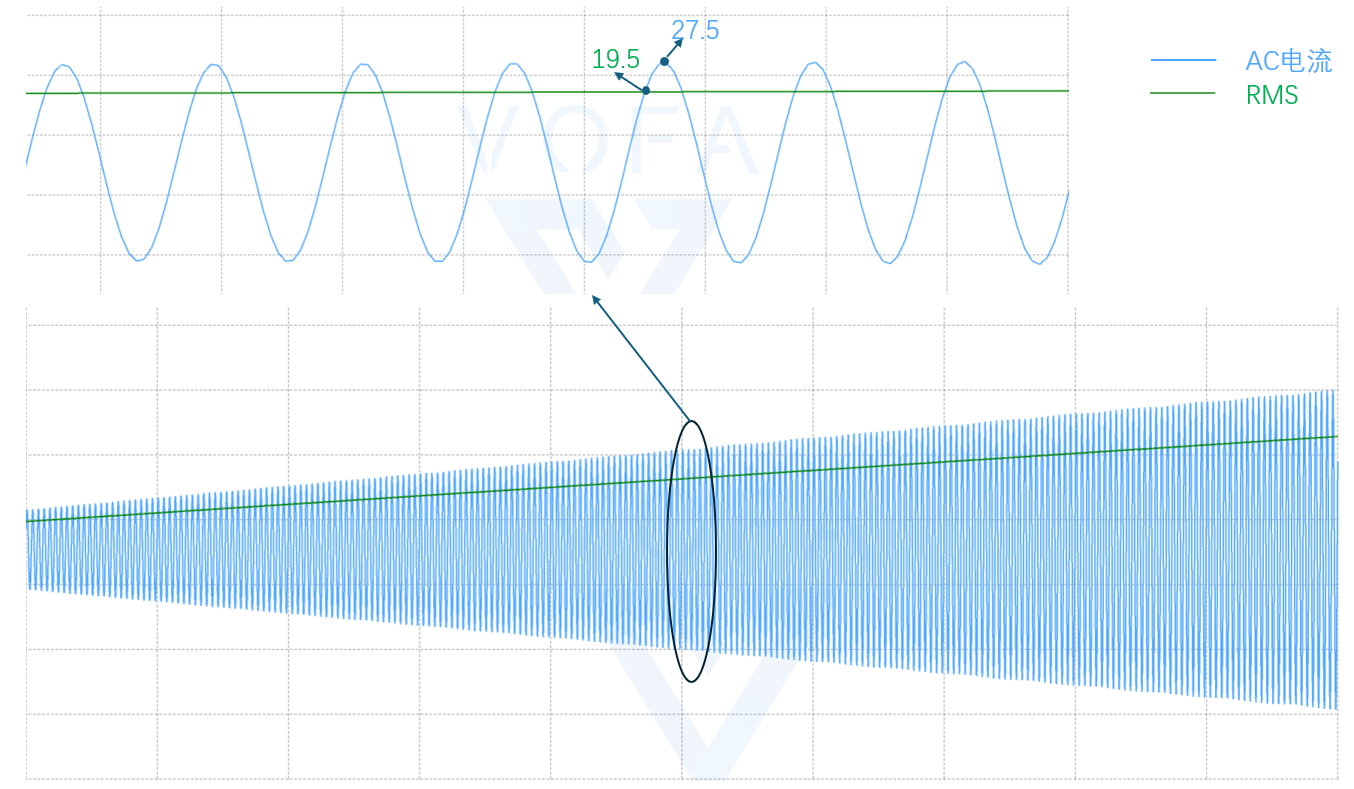
圖中的藍色曲線代表了交流(AC)電流的波形,綠色直線表示計算得到的AC電流的均方根(RMS)值,從圖中可以看出,RMS值在交流電流的一個周期內保持相對穩定,這表明計算方法能夠準確捕捉到AC電流的有效值。圖中標註了AC電流的峰值,分別為19.5和27.5。RMS值與最大峰值保持根號2倍的關係。從圖中RMS值與AC電流波形的跟隨程度來看,遞歸算法在計算RMS值時表現出了良好的準確性和穩定性。這意味著算法能夠有效地處理實時數據,並為PFC應用提供可靠的電流有效值。
四.結論
基於遞歸算法的AC電流RMS計算為PFC應用提供了一種高效、實時的解決方案。這種方法不僅提高了PFC的效率和性能,還優化了資源的使用。隨著技術的不斷發展,遞歸算法在AC電流RMS計算中的應用將越來越廣泛,特別是在需要快速響應和資源受限的環境中。